14. 设全集E={x|x是不大于20的质数},若有A∩B
分类:高等数学256字
答 {3,5,11,13};{7,11,13,19}.
因E={2,3,5,7,11,13,17,19},由A∩B=={2,17},则A∪B={3,5,7,11,13,19},故A∩B=A∪B((A∩B)∪(B∩A))={11,13},故A=(A∩B)∪(A∩B)={3,5,11,13},B=(B∩A)∪(A∩B)={7,11,13,19} ...... (共256字) [阅读本文]>>
答 {3,5,11,13};{7,11,13,19}.
因E={2,3,5,7,11,13,17,19},由A∩B=={2,17},则A∪B={3,5,7,11,13,19},故A∩B=A∪B((A∩B)∪(B∩A))={11,13},故A=(A∩B)∪(A∩B)={3,5,11,13},B=(B∩A)∪(A∩B)={7,11,13,19} ...... (共256字) [阅读本文]>>
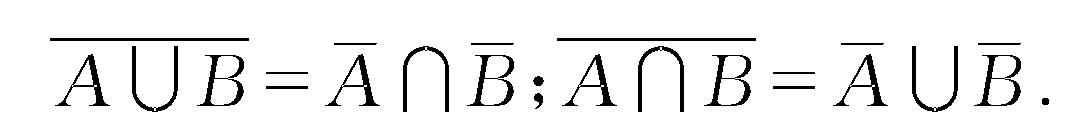 高等数学
高等数学答 对于全集E的任意子集A,B,C,其并、交、补运算有如下基本规律: (1) 交换律 A∪B=B∪A;A∩B=B∩A.(2) 结合律 (A∪B)∪C=A∪(B∪C);(A∩B)∩C=A∩(B∩C).(
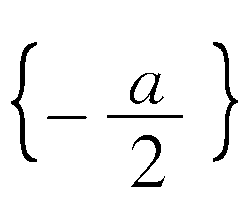 高等数学
高等数学答 -4或-6. 因M={x|2x+a=0}=,P={x|1<x<4且x∈N}={2,3}.又M∩P≠Φ,故M∩P={2}或{3},即=2或=3,即a=-4或-6.
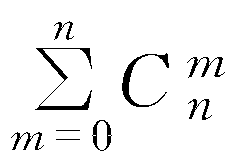 高等数学
高等数学答 2n. 因A的所有由m个元素组成的子集的个数为从n个元素中取m个元素的组合数Cmn.另外,Φ⊂A,所以P(A)的元素N可以表示为:N=1+C1n+C2n+…+Cnn=由二项式定理知:
 高等数学
高等数学解 (1) I1=(2,6].(2) I2=[0,+∞).(3) I3=(-3,3).(4) 由|x-3|≤4⇒-1≤x≤7,则I4=[-1,7].(5)
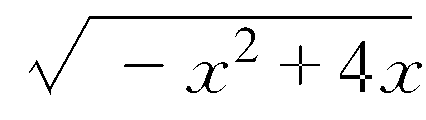 高等数学
高等数学答 C. 因x∈[0,4],有-x2+4x=-(x-2)2+4∈[0,4],于是∈[0,2].则 y=2-故选C.