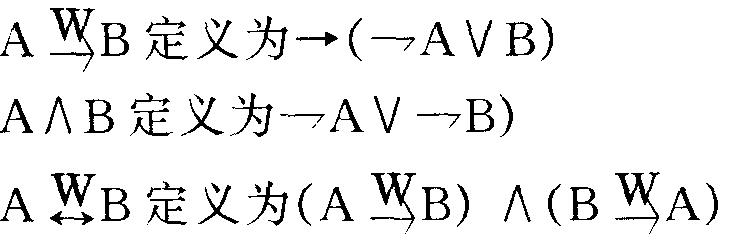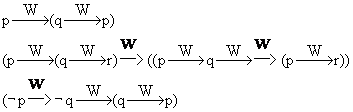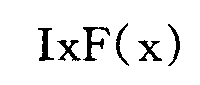是一种用于数字图象处理和识别的新理论和新方法。1965年，前联邦德国和法国巴黎矿业学院的科学家们几乎同时奠定了这门新学科的基础，并共同组建了枫丹白露数学形态学研究中心。1973年马瑟荣在他的《Ensemblesaleatoires etgeometrie integrale》一书中严谨而详尽地论证了随机集和积分几何，为数学形态奠定了交通规则实的理论基础。
数学形态学的主要内容是设计一整套变换(运算、概念和运算，借助于面积、周长、连通分支的数目、曲率半径、“大小分布”等一系列几何参数，采用可间接测量各种几何参数及反映图形体现视性质的积分几何和适于描述图象随机性质的随机集论等数学工具，来确定图象的基
...... （共424字） [阅读本文]>>
西方思想斯多葛学派的主要领袖。他的浩瀚的著作奠定了这个学派的理论基础，甚至可以说，“如果没有克里西普斯，也就没有斯多葛学派”。他十分勤奋，据说每天必写五百行，一生共有七百零五种著作(包括编纂和重复的)。他关于
西方思想数理逻辑共使用五个命题联结词：∧(合取)、∨(析取)、(蕴涵)、(等值)、⇁(否定)、但并不是每个联结词都是必不可少的。一个系统根据自己的需要，可以选择其中的两个作为初始的联结词，把其他三个通过定义的
西方思想亦称命题演算。指处理复合命题及其逻辑关系，并将所有的重言式(其值党真的命题，如P∨⇁P)，组成一个完全形式化的符号系统。与谓词逻辑不同，命题逻辑在研究和考查逻辑形式时，将一个命题只分析到其中所含的命题
西方思想指研究包含模态词“必然”、“可能”的模态命题及其推理的科学。早在二千多年前，亚里士多德在它的《工具论》一书中，就对模态命题作过大量的讨论，并提出了许多模态三段论的推理形式。本世纪初，美国逻辑学家刘易斯
西方思想指研究摹状词的特征性质和使用方法的逻辑学说。摹状词是描述满足某种条件的、存在一个并且仅仅存在一个的那种事物时所使用的数理逻辑名词。在日常生活和科学研究中，经常会涉及到一些具有唯一性的事物，如“法国的首
上一篇