二次效用函数
分类:投资192字
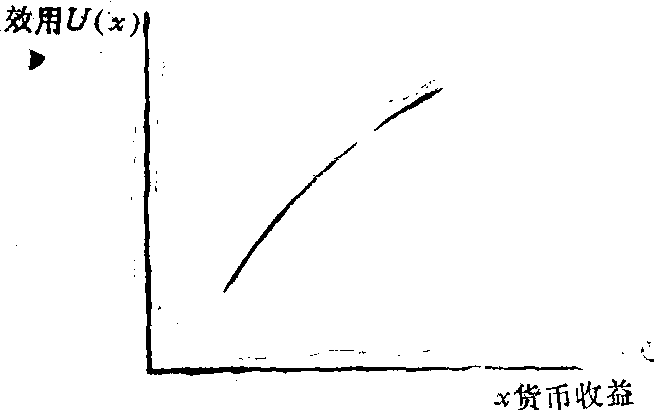
函数形式为二次多项式的效用函数即为二次效用函数。它可以是U(x)=A(x)-B(x)2,效用曲线呈向上倾斜的下凹形,表示决策者厌恶风险的决策倾向,也可以是U(x)=A(x)+B(x)2,效用曲线呈向上倾斜的上凸形,反映决策者偏好风险的决策特性。
[参]风险规避型效用函数、风险偏好型效用函数
U(x)=A(x)-B(x)2
U(x)=A(x)+B(x) ...... (共192字) [阅读本文]>>

函数形式为二次多项式的效用函数即为二次效用函数。它可以是U(x)=A(x)-B(x)2,效用曲线呈向上倾斜的下凹形,表示决策者厌恶风险的决策倾向,也可以是U(x)=A(x)+B(x)2,效用曲线呈向上倾斜的上凸形,反映决策者偏好风险的决策特性。
[参]风险规避型效用函数、风险偏好型效用函数
U(x)=A(x)-B(x)2
U(x)=A(x)+B(x) ...... (共192字) [阅读本文]>>
 投资
投资分析一个自变量与一个因素之间的关系,进行预测的方法。如果一个因变量的变化主要取决于某一自变量,而且相互间的数据分布呈线性趋势,可以用一元线性回归预测方程:yc=a+bx进行预测。一元线性回归预测与直线趋
 投资
投资此法是在X与Y两变量呈线性关系时采用的一种定量预测技术。通过对大量统计数据的观察与分析,若发现因变量Y(即预测目标变量)随自变量X(即影响预测目标的因素)按线性规律变化时,则可建立线性回归方程Y=a+b
 投资
投资此法属于时间序列的指数平滑预测法,是在移动平均预测法基础上发展起来的。它既具有移动平均法的长处,又可减少了运算过程中数据的存储量,同时还充分考虑了时间序列数据的远近期的不同影响。其实质也是求一个加权平均
 投资
投资一阶线性差分方程的一般形式为:y(t)=by(t-1)+a其中a和b为常数。它的求解公式为:y(t)=y(0)+atb=1若无初始条件,令任意常数A=y(0)-a/(1-b)(当b≠1时),或A=y(0
 投资
投资形如:y′+P(x)y=Q(x)的方程,称一阶线性方程。它的通解是:式中的第二项Ce-Sp(x)dx是对应齐次方程的通解,第二项y′+p(x)y=0是原来非齐次方程的一个特解(在通解中令C=0便得到这个