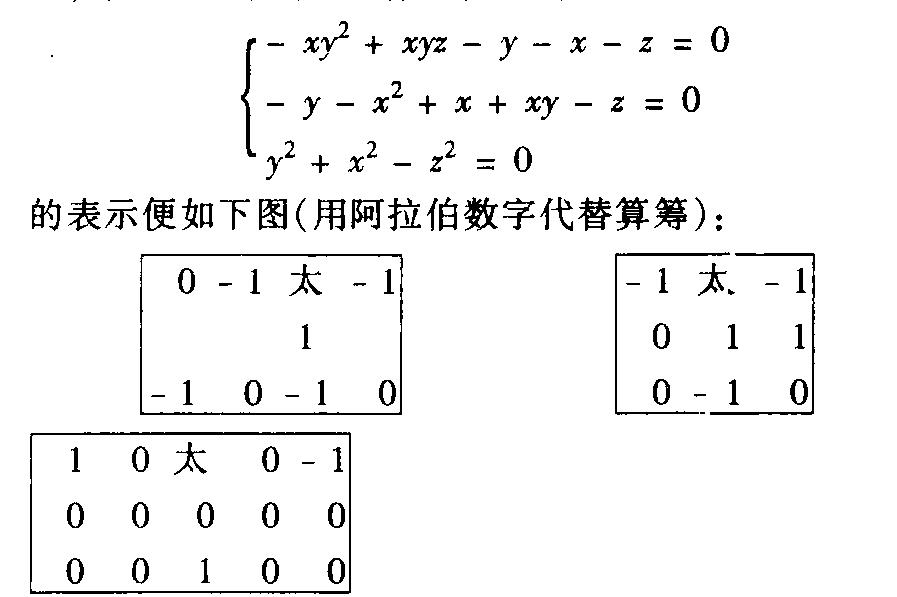
金元数学家创造的重要数学方法，即今之多元高次方程组解法。根据祖颐在《四元玉鉴后序》(公元1303年)中记载，天元术产生之后，“平阳(今山西省临汾)李德载因撰《两仪群英集臻》兼有地元，霍山邢先生颂不高弟刘大鉴润夫撰《乾坤括囊》，末仅有人元二问，吾友燕山朱汉卿先生演数有年，探三才之赜，索《九章》之隐，按天、地、人、物立成四元。”朱世杰不仅是四元术的创造者，而且他的《四元玉鉴》也是保存到今天的使用二元术、三元术、四元术的唯一著作。四元术包括四元表示法和四元消法两部分内容。四元表示法是将常数项居中，旁记一“太”字，天元的系数居下，地元居左，人元 ...... （共579字） [阅读本文]>>
中华国粹即今之线性方程组解法，古代一项重大创造及重要数学方法。九数之一，构成《九章算术》第八章。刘徽说：“群物总杂，各列有数，总言其实。令每行为率，二物者再程，三物者三程，皆如物数程之。并列为行，故谓之方程。行
中华国粹古称勾股术，西方称为毕达哥拉斯定理。中国古代数学创造之一，虽晚于古希腊，但在用于解勾股形方面，却超过了后者。《九章算术》提出：“勾股术曰：勾股各自乘，并而开方除之，即弦。又股自乘，以减弦自乘，其余开方除
中华国粹满足勾股方程a2+b2＝c2的有理数组(a，b，c)称为勾股数，西方称为毕达哥拉斯数。古希腊的毕达哥拉斯、柏拉图、欧几里得等大数学家都试图找出能满足上述方程的所有数组的表达式，即勾股数通解公式，但都只是
中华国粹又称幻方，古代数学创造之一。从1到n2的自然数排列成纵横各有n个数的正方形，使每行、每列及对角线上的n个数的和都等于1/2n(n2+1)，便称为n阶纵横图。东汉郑玄(公元129～200年)注《易纬·乾凿
中华国粹古代用于开方的一种算表，西方称作帕斯卡三角(公元1665年)，今中学课本误作杨辉三角。11世纪北宋数学家贾宪所创造。贾宪是北宋大天文历算学家楚衍的学生，曾任左班殿直，著《黄帝九章算经细草》九卷、《算法&
上一篇