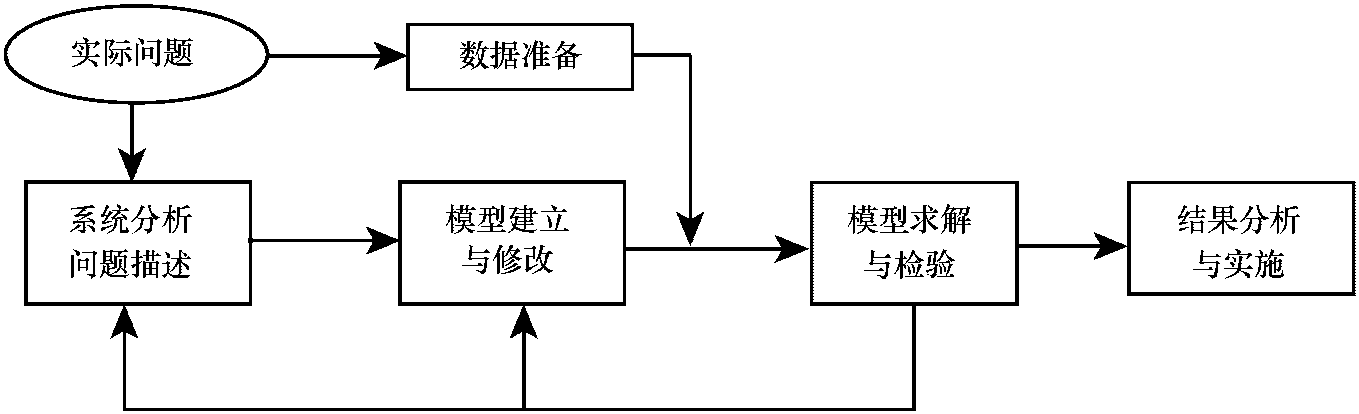
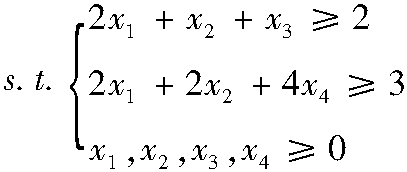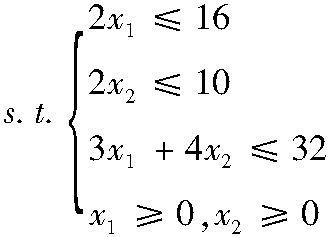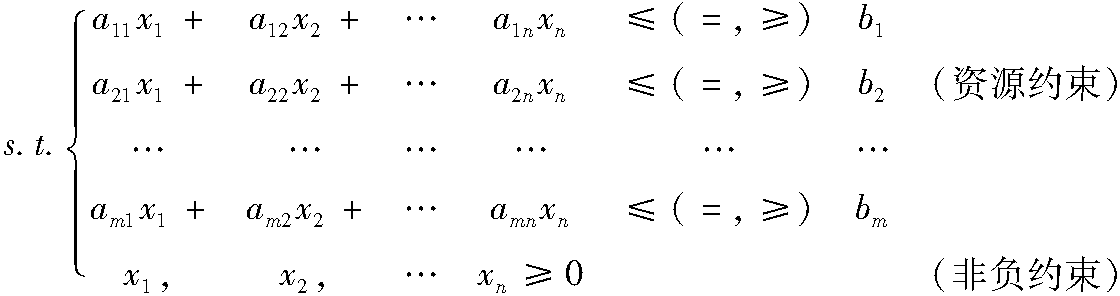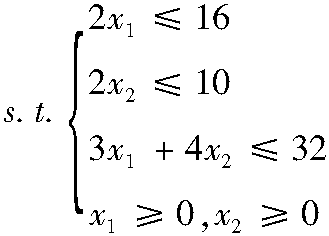3.2.3 解的性质
基本定理: 对于标准型线性规划: ①若有可行解,则必有基本可行解; ②若有最优解,则必有基本最优解 (即既是基本解又是最优解)。
定理的意义: 本定理告诉我们,寻找线性规划的最优解,无须在全部可行解 (一般有无穷多) 中去寻找,而只需在有限个基本可行解 (至多Cmn个) 中去寻找,故当Cmn不大时,可通过比较全部基本可行解的目标值而求出最优解。
退化解: 一个基本解中如果存在取零值的基变量,则该解称作退化的基本可行解,该解对应的基称作退化基。如果有关的线性规划问题的所有基本可行解都是非退化解,则该问题称作非退化的线性规划问题。
由于退化会引起线性规划求解的困难, ...... (共382字) [阅读本文]>>

 上一篇
上一篇