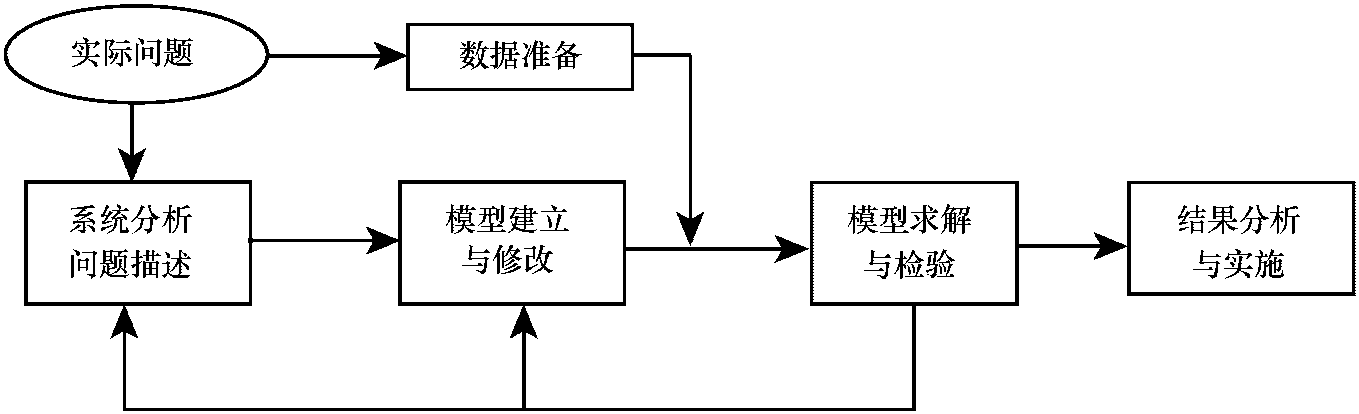
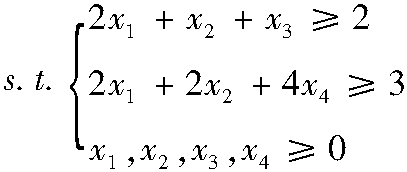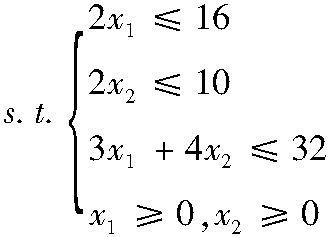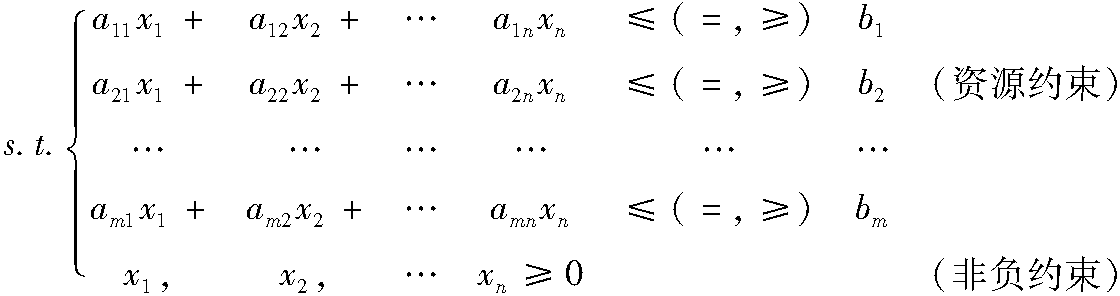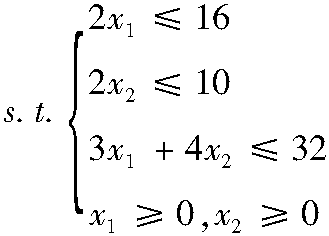3.2.2 基本可行解及有关概念

要掌握LP问题的一般解法,首先必须理解以下概念。
(1) 基 (basis): A中m×m子矩阵B并且有r (B) =B,则称B是线性规划的一个基 (或基矩阵basis matrix)。当m=n时,基矩阵唯一,当m<n时,基矩阵就可能有多个,但数目不会超过Cmn。
由线性代数知,基矩阵B必为非奇异矩阵并且|B| ≠0。
(2) 向量。当确定某一矩阵为基矩阵时,则基矩阵对应的列向量称为基向量 (basisvector),其余列向量称为非基向量。向量通常用pj表示。
基向量对应的变量称为基变量 (basis variable),非基向量对应的变量称为非基变量。通常用xB表示基变量,用xN表示非基变量。
例:
如果取:B=(p2,p3)=(),则|B|=2-6=-4≠0,故此B是一个基,对于此B而言,xB ...... (共1274字) [阅读本文]>>

 上一篇
上一篇