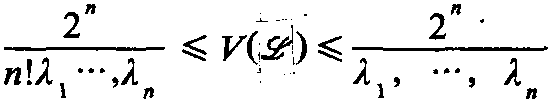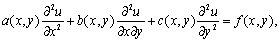研究无穷维线性空间上算子及其泛函的分析学科。泛函分析的基本概念建立于本世纪20年代，而作为一门独立学科则形成于30年代。它是从变分法、微分方程、积分方程、函数逼近论及其量子物理学中逐渐发展起来的，泛函分析主要采用几何、代数的方法研究分析学的问题，因此可以把它看作无穷维分析学。它是研究无穷个自由度的物理系统，诸如连续介质力学、电磁场理论等的有力工具。
泛函分析的某些概念可以追溯到微积分的发现，因为微分是作用在可微函数类上的算子，积分是定义于可积函数类上的泛函。但泛函分析的真正起源是斯特姆 (C.F.Sturm，1803～1855) 利乌维尔 (J.Liou ville，1809～1882) 理论 ...... （共1393字） [阅读本文]>>
自然科学学科用几何方法研究某些数论问题的数学理论。又称几何数论，数论的分支学科。是研究丢番图逼近、代数数论的重要工具。它的一类典型问题为：设f(x1，…，xn)是实变量x1，…，xn的实值函数，则对适当选取的整数u
自然科学学科含有未知函数的偏导数的方程称为偏微分方程，是微分方程的分支。含于方程中的偏导数的最高阶称方程的阶。例如，即为关于未知函数u(x，y)的二阶偏微分方程。二阶线性与非线性偏微分方程始终是重要的研究对象。这类
研究现实世界中数量关系和空间形式的科学。简言之，数学是研究数和形的科学。它的特点是：抽象性、精确性和应用的广泛性。数学的抽象性表现在它暂时撇开事物的具体内容而单纯从量的关系来考察;精确性表现在它的逻辑的
研究数的规律，特别是研究整数规律的科学。数学的分支学科。数论以可除性、同余性、不定方程的求解和数的有理逼近等算术问题为研究对象，是两个最古老的数学分支之一(另一个是经典的欧氏几何)。正整数分成1、素数和
用分析方法研究整数的性质和素数分布规律的科学。数论的分支学科。解析数论以素数分布、格点问题和堆垒数论中的问题为主要的研究对象。一般说来，凡是用分析方法研究的数论问题都可归结为解析数论，解析数论的内容十分
上一篇