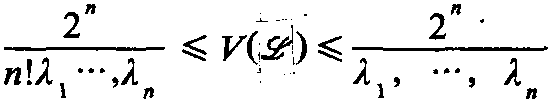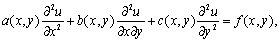研究泛函的极值的方法。它的核心问题是求泛函的极值函数和相应的极值。与函数极值类似，变分法的基本问题是确定极值的必要条件和充分条件。
物理学中泛函极值问题的提出促进了变分学的建立和发展，而变分学的理论成果则不断渗透到物理学中，在许多数学物理的分支，如弹性力学、电磁理论、相对论、量子理论中建立了变分原理。它从一个侧面反映了客观世界的统一性。此外，变分法对解许多实际物理问题也提供了切实可行的方法，如可用变分法解振动系统的本征频率问题、散射问题等。基于变分原理还建立了偏微分方程的弱解的L2理论及相应的有限元解法和其它直接解法。
作为20世纪变分 ...... （共370字） [阅读本文]>>
自然科学学科用几何方法研究某些数论问题的数学理论。又称几何数论，数论的分支学科。是研究丢番图逼近、代数数论的重要工具。它的一类典型问题为：设f(x1，…，xn)是实变量x1，…，xn的实值函数，则对适当选取的整数u
自然科学学科含有未知函数的偏导数的方程称为偏微分方程，是微分方程的分支。含于方程中的偏导数的最高阶称方程的阶。例如，即为关于未知函数u(x，y)的二阶偏微分方程。二阶线性与非线性偏微分方程始终是重要的研究对象。这类
研究现实世界中数量关系和空间形式的科学。简言之，数学是研究数和形的科学。它的特点是：抽象性、精确性和应用的广泛性。数学的抽象性表现在它暂时撇开事物的具体内容而单纯从量的关系来考察;精确性表现在它的逻辑的
研究数的规律，特别是研究整数规律的科学。数学的分支学科。数论以可除性、同余性、不定方程的求解和数的有理逼近等算术问题为研究对象，是两个最古老的数学分支之一(另一个是经典的欧氏几何)。正整数分成1、素数和
用分析方法研究整数的性质和素数分布规律的科学。数论的分支学科。解析数论以素数分布、格点问题和堆垒数论中的问题为主要的研究对象。一般说来，凡是用分析方法研究的数论问题都可归结为解析数论，解析数论的内容十分
上一篇