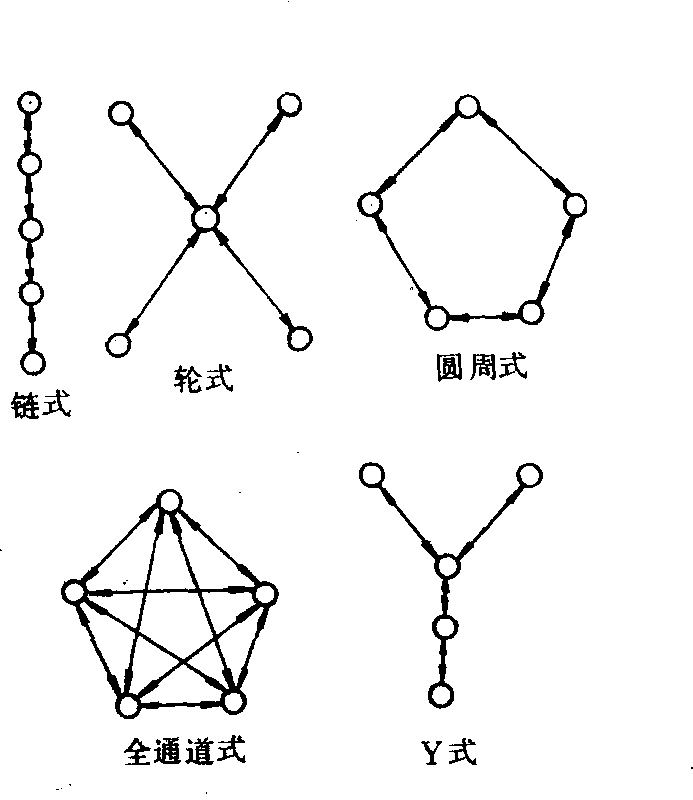
牛顿法
也称切线法。是一维搜索法的一种具体算法,因以函数切线作为确定试算点和近似逼近最优解数列的依据而得名。运用条件为:(1)目标函数在区间[a,b]上的二阶导数存在且不变号。(2)只有一个极值点。计算步骤为:(1)确定精度要E>0,任取初始点x0∈[a,b]。(2)判断丨f′xk)丨≤E,若是,则xk即为近似最优解。否则有(3)取xk+1=xk-f′(xk)/f″(xk),转(2)。这一算法中,初始点x0的选取将影响收敛性,且要保证上述条件(1)也是困难的 ...... (共231字) [阅读本文]>>

 上一篇
上一篇