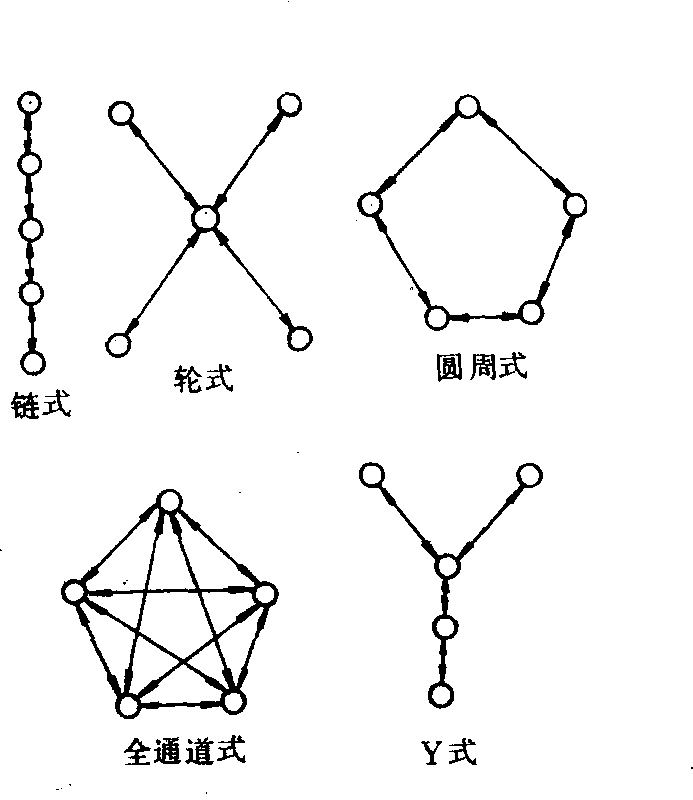
斐波那契法
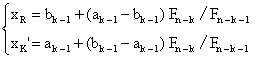
求非线性最优化问题的一种确定试算点的方法。设要求近似极值点ao,bo的精度为δ,则丨b-au丨(b-a)≤δ,为计算终止的依据。因取斐波那契数列{Fn}:F0=F1=1,Fk-1=Fk+Fk-1,(k=1,2,…)作为确定试算点而得名。基本步骤为:(1)由Fu≥1/s确定试算点的个数n。(2)选取试算点:x1=a+(b-a)Fu-2/Fu,x′1=a+(b-a)Fn-1/Fn。(3)若f(x1)<f(x′1),则取a1=a,b1=x′1,x′2=x1,并令x2=b1=(b1-a1)Fn-2/F-1,否则取a1=x1,b1=b,x2=x′1,并令X′2=a1+F-2(b1-a1)/Fn-1。(4)计算f(x′2)或f(x2),如第三步那样一步步迭代,计算试算点的公式为:
取f(xk-1)或f(x′u-1)为近似最优值,xn-1或x′n-1为近似最优解 ...... (共386字) [阅读本文]>>
 上一篇
上一篇