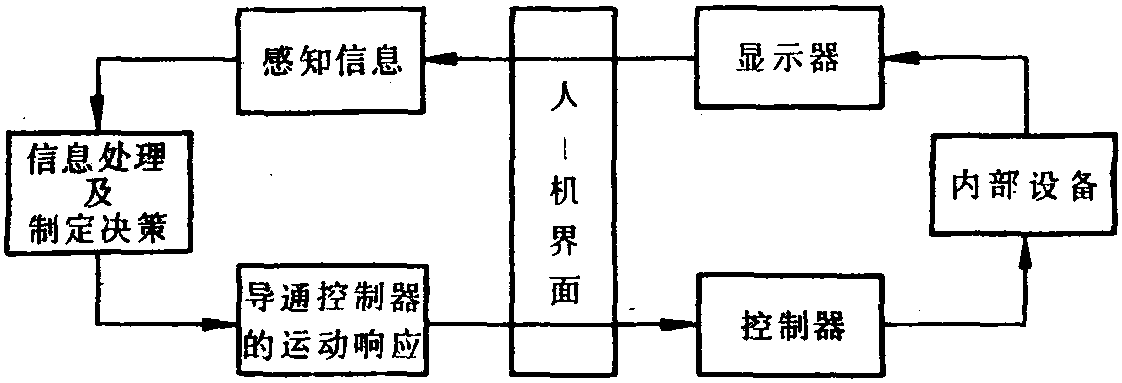
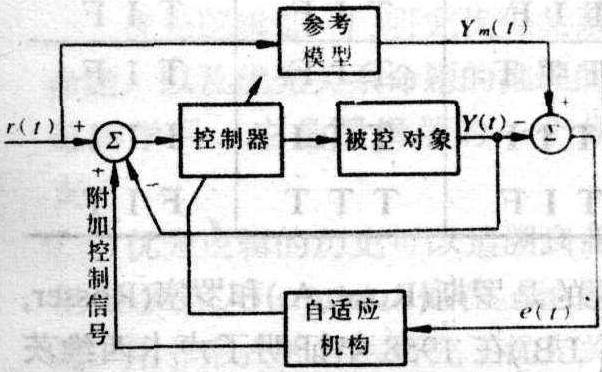
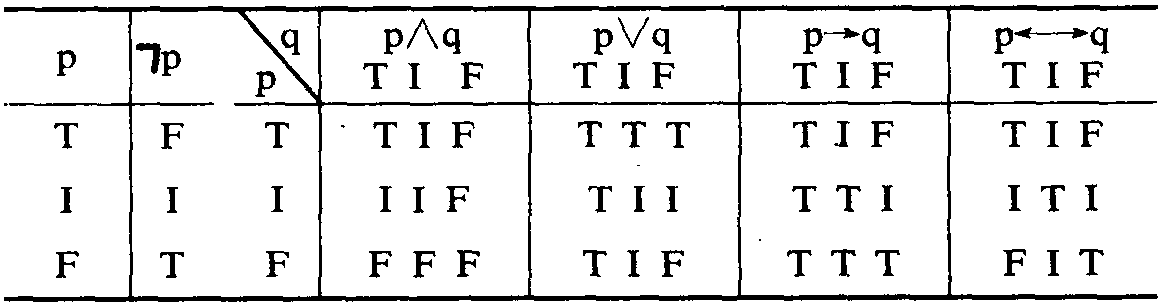
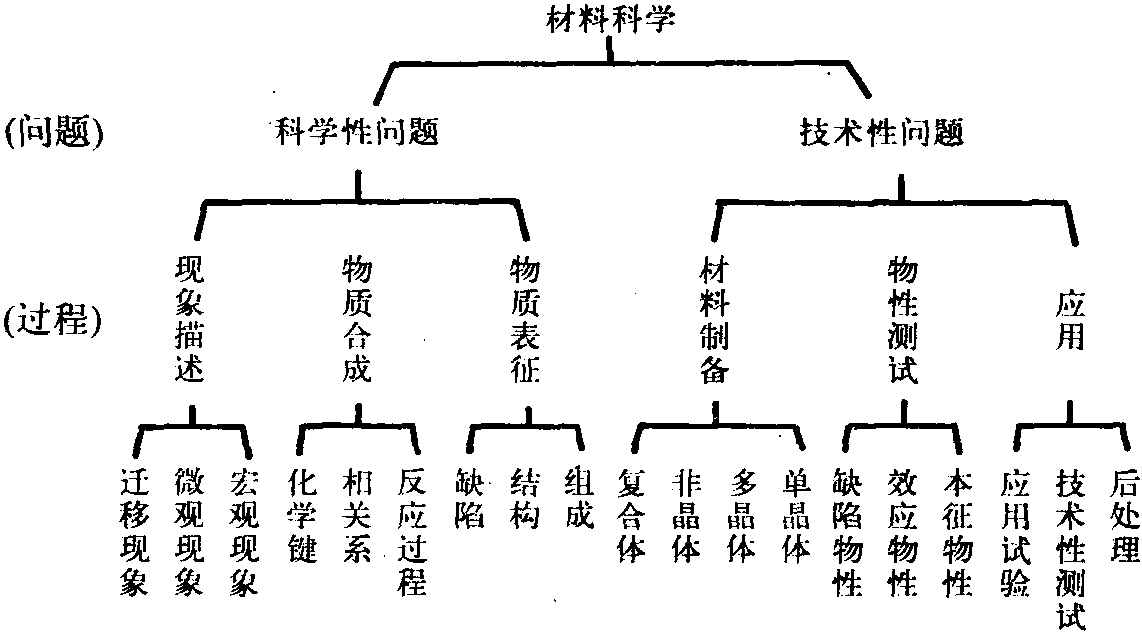
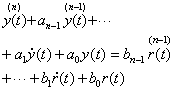矩阵论是一门研究矩阵运算性质及其应用的线性代数的分支学科。所谓矩阵是指环或域k(通常以实数域R或复数域c作为k)中的mn个元素aij(i=1，…… m;j=1，……，n)排列成如下的一个矩形阵列：
简记为(aij)或A。若m=n，则称为n阶方阵。aij＝0(i≠j)的方阵称为对角矩阵。aij＝1且aij＝0(i≠j)的方阵称为单位矩阵，用I表示。
矩阵的研究开始于18世纪中叶，而真正成为一门科学是19世纪末的事情。矩阵论的创立应归功于凯莱(Cayley)和西勒维斯特(Sylvester)。他们从1850年开始相继发表了大量的研究文章，从而奠定了矩阵论的基础。
矩阵可以看作数的推广，其运算适合普通代数的某些规则，但不是所有规则。
两个矩阵A=(aij) ...... （共1415字） [阅读本文]>>
现代学科人-机系统是研究在一定的环境条件下、为达到某些整体性目标而存在交互作用的人和机的组合的学科，属于工程控制论与生物医学工程等基本学科中的交叉学科。人-机系统的组成原理图在下图中示出。人-机系统组成原理图图
现代学科自适应控制是一门研究具有不确定性系统控制问题的学科。它是“工程控制论”基本学科中的一个分支学科。由于自适应控制适用的领域很广，加上有些系统的自适应控制律与非线性或时变控制律没有明显的界限，因此自适应控制
现代学科多值逻辑是一门研究具有有穷或无穷多个真值的命题的逻辑演算，以及这些演算的逻辑性质的逻辑学科。它是现代逻辑的一个分支。古希腊亚里士多德(Aristotle)曾经讨论过命题除“真”“假”之外的另一种真值“未
现代学科材料科学是研究材料的化学组成、结构及其特性，并在此基础上研制具有性能和新功能的新型材料及其应用的一门科学。材料科学是20世纪60年代才发展起来的一门新学科。近代化学和物理学的发展，为揭示物质本质的奥秘提
现代学科经典控制理论是一门研究单输入单输出线性时不变反馈控制系统的学科，它属于工程控制论基本学科中的一个分支学科。自动控制理论是自动化技术的基础理论，按它的发展过程大致可划分为经典控制理论、现代控制理论和大系统
上一篇