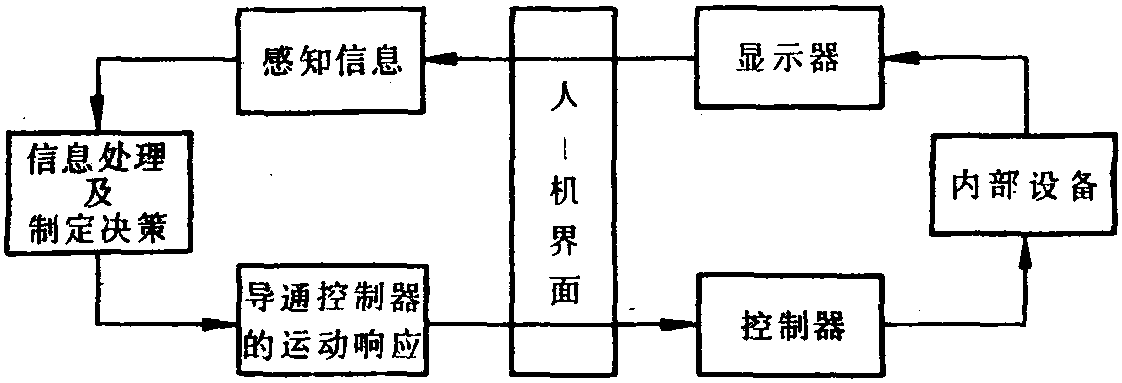
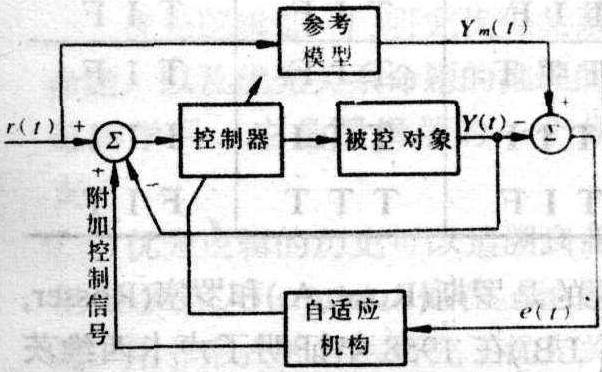
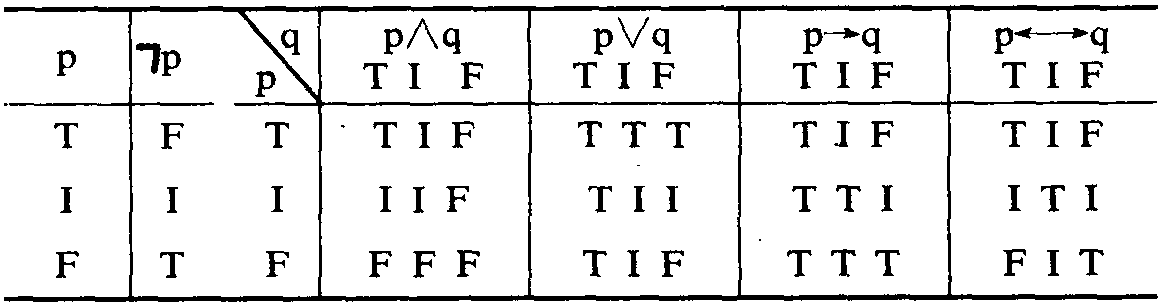
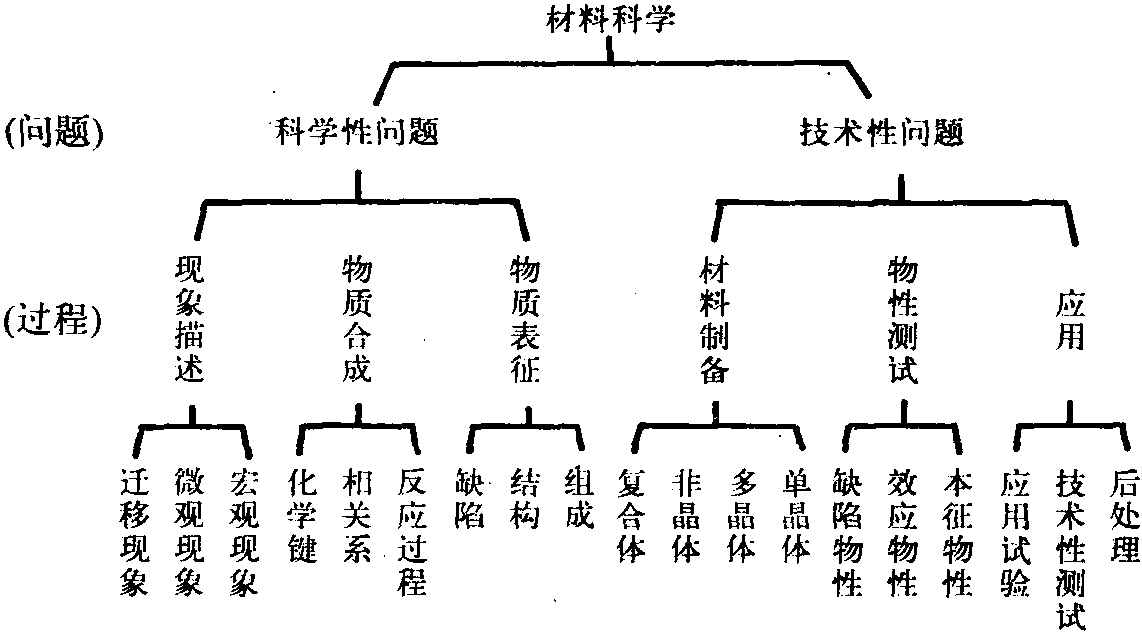
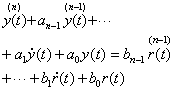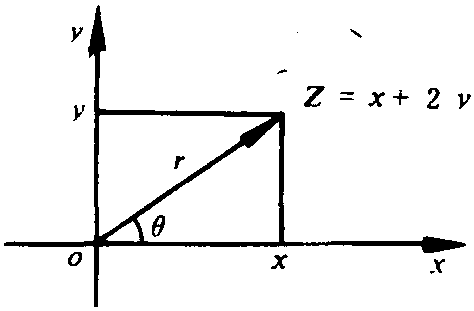
复变函数论是一门研究以复数为自变量函数的性质，理论及其应用的数学分支。
形如z=x+iy或z=x+yi的数，称为复数，其中x，y为任意实数，分别称为复数z的实部与虚部。i(i2＝-1)称为虚数单位。复数可用复平面表示
x——实轴
y——虚轴
——称为z的模
θ=Argz——z的幅角
复变函数W=f(z)，把复平面变为复平面
复变函数论的形成经过比较漫长和曲折的过程。16世纪中叶意大利数学家卡尔丹(Cardan，H.)在解三次方程时，首先产生了负数开平方的思想，他把40看作5的乘积，这种形式的数，即今天讲的复数，在当时被认为是不能接受的“虚数”。直到17世纪和18世纪，随着微积分的发明与发展，才发生了观念的改变。尤其 ...... （共1069字） [阅读本文]>>
现代学科人-机系统是研究在一定的环境条件下、为达到某些整体性目标而存在交互作用的人和机的组合的学科，属于工程控制论与生物医学工程等基本学科中的交叉学科。人-机系统的组成原理图在下图中示出。人-机系统组成原理图图
现代学科自适应控制是一门研究具有不确定性系统控制问题的学科。它是“工程控制论”基本学科中的一个分支学科。由于自适应控制适用的领域很广，加上有些系统的自适应控制律与非线性或时变控制律没有明显的界限，因此自适应控制
现代学科多值逻辑是一门研究具有有穷或无穷多个真值的命题的逻辑演算，以及这些演算的逻辑性质的逻辑学科。它是现代逻辑的一个分支。古希腊亚里士多德(Aristotle)曾经讨论过命题除“真”“假”之外的另一种真值“未
现代学科材料科学是研究材料的化学组成、结构及其特性，并在此基础上研制具有性能和新功能的新型材料及其应用的一门科学。材料科学是20世纪60年代才发展起来的一门新学科。近代化学和物理学的发展，为揭示物质本质的奥秘提
现代学科经典控制理论是一门研究单输入单输出线性时不变反馈控制系统的学科，它属于工程控制论基本学科中的一个分支学科。自动控制理论是自动化技术的基础理论，按它的发展过程大致可划分为经典控制理论、现代控制理论和大系统
上一篇