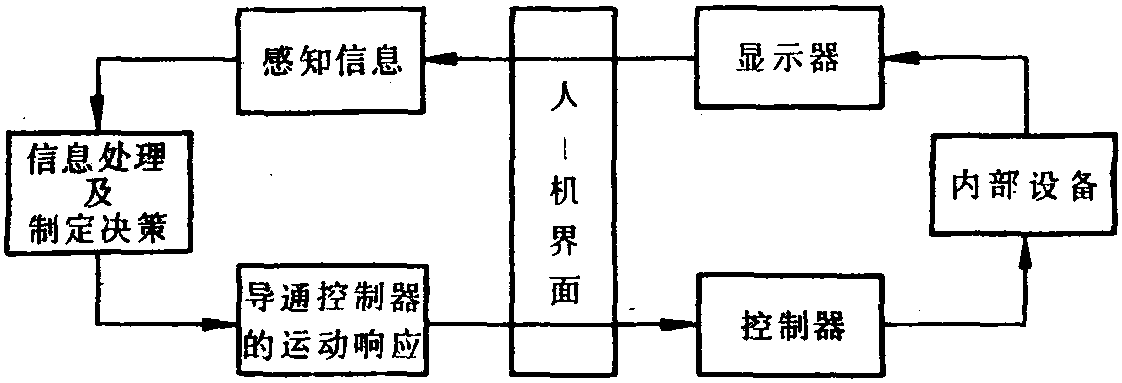
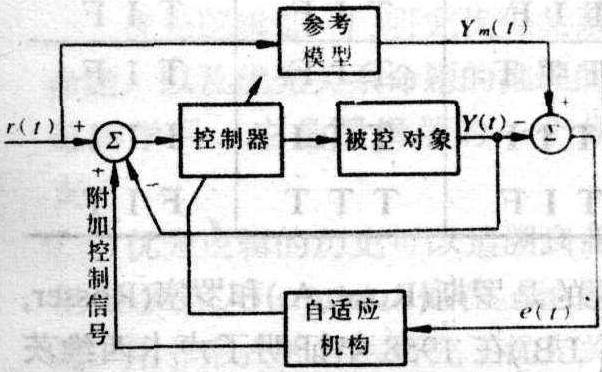
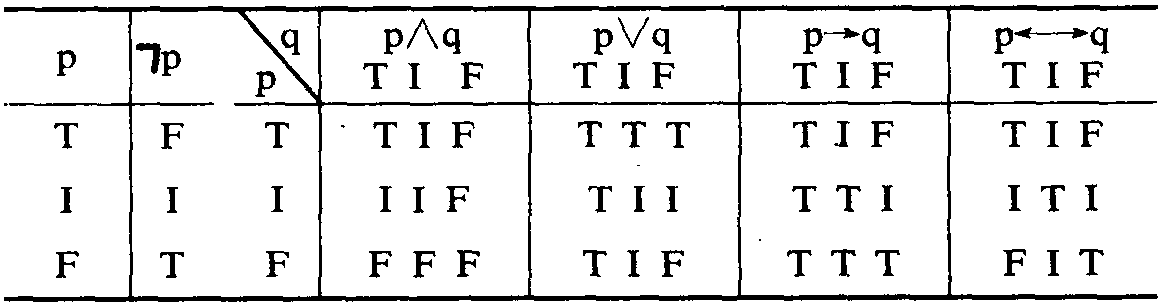
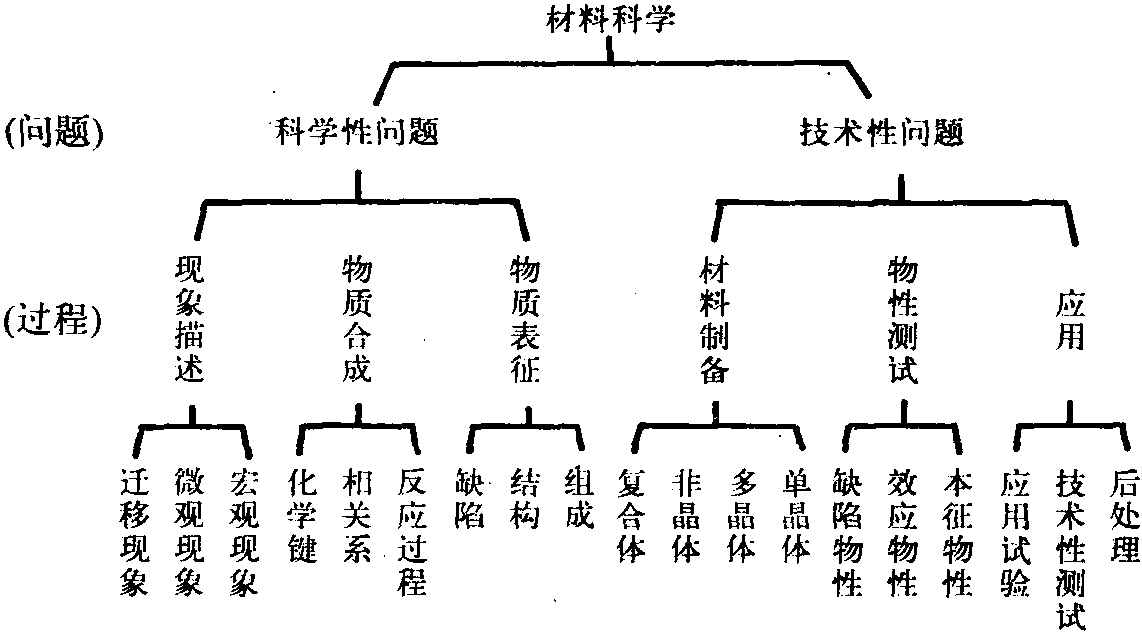
一般拓扑学也称点集拓扑学，是研究抽象空间及空间中图形在连续变形下各种不变性质的数学理论。它和代数拓扑学一起，构成拓扑学的两大分支。
拓扑学的基础是集合论，但在康托 (Cantor，G.) 的集合论中，不涉及点与点之间的连系。1906年弗雷歇，莫 (Fréchet，M) 为了将康托的集合论和函数空间统一起来，致力于抽象空间的研究，并指出点与点之间的联系可以不是欧氏空间中的距离函数。豪斯道夫.费(Hausdorf.F) 在1914年出版的《点集论基础》 (Grundzüge der Mengen-Lehre) 一书中采用邻域概念建立了拓扑空间的完整理论。
根据豪斯道夫的定义，对集合X，用T记X的一个子集族，如果
(1)T中任意个元素之并仍在T中 ...... （共1261字） [阅读本文]>>
现代学科人-机系统是研究在一定的环境条件下、为达到某些整体性目标而存在交互作用的人和机的组合的学科，属于工程控制论与生物医学工程等基本学科中的交叉学科。人-机系统的组成原理图在下图中示出。人-机系统组成原理图图
现代学科自适应控制是一门研究具有不确定性系统控制问题的学科。它是“工程控制论”基本学科中的一个分支学科。由于自适应控制适用的领域很广，加上有些系统的自适应控制律与非线性或时变控制律没有明显的界限，因此自适应控制
现代学科多值逻辑是一门研究具有有穷或无穷多个真值的命题的逻辑演算，以及这些演算的逻辑性质的逻辑学科。它是现代逻辑的一个分支。古希腊亚里士多德(Aristotle)曾经讨论过命题除“真”“假”之外的另一种真值“未
现代学科材料科学是研究材料的化学组成、结构及其特性，并在此基础上研制具有性能和新功能的新型材料及其应用的一门科学。材料科学是20世纪60年代才发展起来的一门新学科。近代化学和物理学的发展，为揭示物质本质的奥秘提
现代学科经典控制理论是一门研究单输入单输出线性时不变反馈控制系统的学科，它属于工程控制论基本学科中的一个分支学科。自动控制理论是自动化技术的基础理论，按它的发展过程大致可划分为经典控制理论、现代控制理论和大系统
