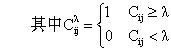是极率论中的一个基本定理。
当我们把极率与语句的性质联系在一起时，就把概率定义为语句代数上的实值函数P。令s，e表示任何语句，T，F表示真和假。
这样若P(e)>0即可定义给定eFS的条件概率P(S/e)=p(S∧e)/P(e)
(1)
显然当e=T时，P(S/e)=P(S)，它表示在真条件下S的条件概率P(S/T)就是它的无条件概率P(S)。
同样当P(S)>0时仿照(1)也可得到
P(e/s)=P(s∧e)/P(s)
(2)
由(1)，(2)可以得到
P(s/e)=p(e/s)·p(s)/p(e)
(3)
这是贝叶斯公式的初步形式。
设S是语句的有限集合，若令s∈S是不可兼折取的语句(不相容)，则
P(e)=P(e∧S)=P(e∧s)=p(e/s)p(s)
(4)
从而由(3)，(4)即可得到
P(s/e)=p(e/s)·p(s)/p(e/s)·p(s)
(5)
(5)式即为贝叶斯定理的一般形式。
贝叶斯定理的
...... （共812字） [阅读本文]>>
方法模糊排序中最常用的方法。所谓排序是针对某种特定含义进行的。例如，在人群中按健康程度排序就是一个典型的模糊排序的例子。二元对比排序，是指对几个特定的排序对象在两面对比的基础上所做的整体排序。常用的二元对比
方法三相模糊统计方法的一种特定方法。将一个论域分成三个模糊区域，关键在于找到二个分界点。例如：〔老，中，青〕的划分，在人的年龄集合〔0，200〕上要找到老年与中年的分界点，用ξ表示。还要找到中年与青年的分界
方法从某种严格的意义上说，内涵逻辑是研究涉及到意义或者意义等同的推理那种逻辑的一部分。它是和外延逻辑相对应的一种逻辑。外延逻辑对其一般原则的陈述和论证仅与下述概念相关：真与假，真值、集合或者类的同一和差异，
方法多重复合判断推理的一种。所有三段论都可以表述为多重复合判断“如果p且q，那么r”。其中p和q相当于三段论的两个前提，r相当于三段论的结论。所谓反三段论是沿着与三段论相反的方向进行的演绎推理。推理过程是首
方法一种构造理论体系的演绎方法。包括两个要点：第一，它在一个理论中明确区分了初始概念和被定义概念，出发命题(即公理)和被证命题(即定理);第二，它明确规定了演绎的规则。运用这些规则于公理和已证定理，就可以证
上一篇