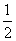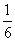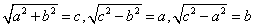勾、股各自乘，并之为弦实。开方除之，即弦。按：弦图，又可以勾、股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实亦成弦实①。以差实减弦实，半其馀，以差为从法，开方除之，复得勾矣。加差于勾，即股②。
凡并勾、股之实即成弦实，或方于内，或矩于外〔原本“矩”“方”互讹，依钱宝琮校〕，形诡而量均，体殊而数齐。勾实之矩以股弦差为广，股弦并为袤③。而股实方其里。减矩勾之实于弦实，开其馀即股④。倍股在两边为从法，开矩勾之角即股弦差。加股为弦⑤。以差除勾实，得股弦并⑥。以并除勾实，亦得股弦差⑦。令并自乘，与勾实为实，倍并为法。所得亦 ...... （共3489字） [阅读本文]>>
中国历代文献精粹衰分术曰：各置列衰，副并为法，以所分乘未并者各自为实，实如法而一。不满法者，以法命之。汉《九章算术·衰分》【评】这是完整的比例分配算法。列衰即是相与率。设所分为A，列衰为ai(i=1，2，…n)，则每一
中国历代文献精粹(环田)术曰：并中外周而半之，以径乘之，为积步。汉《九章算术·方田》【评】这是《九章》提出的圆环的面积公式，历代沿用：S=(l1+l2)d。其中S，l1，l2，d分别是环田面积，外周，中周及径(d=r1
中国历代文献精粹刍童、曲池、盘池、冥谷皆同术。术曰：倍上袤，下袤从之;亦倍下袤，上袤从之，各以其广乘之，并，以高若深乘之，皆六而一。其曲池者，并上中、外周而半之，以为上袤;亦并下中、外周而半之，以为下袤。汉《九章算术·
中国历代文献精粹故折矩以为勾广三，股修四，径隅五。既方之外，半其一矩，环而共盘，得成三、四、五。两矩共长二十有五，是谓积矩。汉《周髀算经》卷上若求邪至日者，以日下为勾，日高为股。勾、股各自乘，并而开方除之，得邪至日。汉
中国历代文献精粹开立方(刘徽注：立方适等，求其一面也。)术曰：置积为实。借一算，步之，超二等。(刘徽注：言千之面十，言百万之面百。)议所得，以再乘所借一算为法，而除之。(刘徽注：再乘者亦求为方幂，以上议命而除之，则立方
上一篇