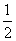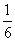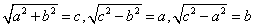今有竹高一丈，末折抵地，去本三尺，问折者高几何?
术曰：以去本自乘，令如高而一，所得，以减竹高，而半馀即折者之高也。
汉《九章算术·勾股》
此去本三尺为勾，折之馀高为股，以先令勾〔原本脱“勾”字〕自乘之幂。凡为高一丈为股弦并，以除此幂得差。此术与系索之类更相反覆也。亦可如上术，令高自乘为股弦并幂，去本自乘为矩幂，减之，馀为实。倍高为法，则得折之高数也。
《九章算术·勾股》三国魏·刘徽注
【评】《九章算术》的题目实际上是已知勾及股弦并求股的问题：b=。刘徽指出它与已知勾及股弦差求股、弦问题的关系，并将公式修正为b=。
股弦和与勾求股法曰：勾自乘为实 ...... （共792字） [阅读本文]>>
中国历代文献精粹衰分术曰：各置列衰，副并为法，以所分乘未并者各自为实，实如法而一。不满法者，以法命之。汉《九章算术·衰分》【评】这是完整的比例分配算法。列衰即是相与率。设所分为A，列衰为ai(i=1，2，…n)，则每一
中国历代文献精粹(环田)术曰：并中外周而半之，以径乘之，为积步。汉《九章算术·方田》【评】这是《九章》提出的圆环的面积公式，历代沿用：S=(l1+l2)d。其中S，l1，l2，d分别是环田面积，外周，中周及径(d=r1
中国历代文献精粹刍童、曲池、盘池、冥谷皆同术。术曰：倍上袤，下袤从之;亦倍下袤，上袤从之，各以其广乘之，并，以高若深乘之，皆六而一。其曲池者，并上中、外周而半之，以为上袤;亦并下中、外周而半之，以为下袤。汉《九章算术·
中国历代文献精粹故折矩以为勾广三，股修四，径隅五。既方之外，半其一矩，环而共盘，得成三、四、五。两矩共长二十有五，是谓积矩。汉《周髀算经》卷上若求邪至日者，以日下为勾，日高为股。勾、股各自乘，并而开方除之，得邪至日。汉
中国历代文献精粹勾、股各自乘，并之为弦实。开方除之，即弦。按：弦图，又可以勾、股相乘为朱实二，倍之为朱实四，以勾股之差自相乘为中黄实，加差实亦成弦实①。以差实减弦实，半其馀，以差为从法，开方除之，复得勾矣。加差于勾，即
上一篇