圆锥
分类:中国历代文献精粹146字
若令其(指方锥)中容圆锥,圆锥见幂①与方锥见幂,其率犹方幂之与圆幂也。
《九章算术·方田》三国魏·刘徽注
[注]①见,读xian,见幂,侧面积。
【评】这里刘徽提出了正确的圆锥侧面积公式,并利用圆锥侧面积:方锥侧面积=π∶4的原理论证了它的正确性,考虑圆锥表面积,在中国古代不多见 ...... (共146字) [阅读本文]>>
若令其(指方锥)中容圆锥,圆锥见幂①与方锥见幂,其率犹方幂之与圆幂也。
《九章算术·方田》三国魏·刘徽注
[注]①见,读xian,见幂,侧面积。
【评】这里刘徽提出了正确的圆锥侧面积公式,并利用圆锥侧面积:方锥侧面积=π∶4的原理论证了它的正确性,考虑圆锥表面积,在中国古代不多见 ...... (共146字) [阅读本文]>>
 中国历代文献精粹
中国历代文献精粹衰分术曰:各置列衰,副并为法,以所分乘未并者各自为实,实如法而一。不满法者,以法命之。汉《九章算术·衰分》【评】这是完整的比例分配算法。列衰即是相与率。设所分为A,列衰为ai(i=1,2,…n),则每一
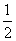 中国历代文献精粹
中国历代文献精粹(环田)术曰:并中外周而半之,以径乘之,为积步。汉《九章算术·方田》【评】这是《九章》提出的圆环的面积公式,历代沿用:S=(l1+l2)d。其中S,l1,l2,d分别是环田面积,外周,中周及径(d=r1
 中国历代文献精粹
中国历代文献精粹刍童、曲池、盘池、冥谷皆同术。术曰:倍上袤,下袤从之;亦倍下袤,上袤从之,各以其广乘之,并,以高若深乘之,皆六而一。其曲池者,并上中、外周而半之,以为上袤;亦并下中、外周而半之,以为下袤。汉《九章算术·
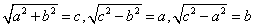 中国历代文献精粹
中国历代文献精粹故折矩以为勾广三,股修四,径隅五。既方之外,半其一矩,环而共盘,得成三、四、五。两矩共长二十有五,是谓积矩。汉《周髀算经》卷上若求邪至日者,以日下为勾,日高为股。勾、股各自乘,并而开方除之,得邪至日。汉
 中国历代文献精粹
中国历代文献精粹勾、股各自乘,并之为弦实。开方除之,即弦。按:弦图,又可以勾、股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实亦成弦实①。以差实减弦实,半其馀,以差为从法,开方除之,复得勾矣。加差于勾,即