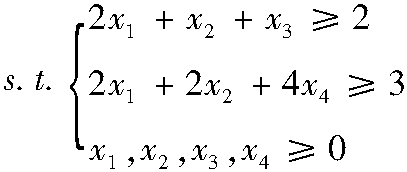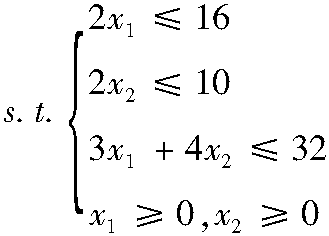两阶段法是把一般线性规划问题的求解过程分为两个阶段。即：
第一阶段： 在原线性规划问题中引入人工变量，并构造仅含有人工变量的目标函数，使其目标函数最小化，用单纯形法求解，以去掉人工变量。若第一阶段求得最优解对应的最优值等于零，则所有人工变量一定取零，说明原问题存在基可行解，可以进行第二阶段计算，否则原问题无基可行解，应停止计算。
第二阶段： 求原问题最优解。在第一阶段计算得的最终单纯形表基础上，恢复原来的目标函数，去掉人工变量所在的列，以第一阶段的最优解为初始基可行解，再用单纯形法继续求解，得到原问题的最优解。
【例3-5】 用两阶段法求 【 ...... （共1515字） [阅读本文]>>
管理运筹学运筹学的分析步骤一般包括：发现和定义待研究的问题，构造数学模型;寻找经过模型优化的结果，并通过应用这些结果来改善系统的运行效率。具体步骤如图1-1所示。1.系统分析和问题描述应用运筹学的主要目的是解决实
管理运筹学运筹学是一门以训练逻辑思维为主的课程，注重模型和定量分析方法，但又不是运筹数学;具有很强的实践性，注重原理、方法和应用，教学中对理论推导可不做过高要求。学生创造性思维培养离不开逻辑思维，但学习过程中也不
管理运筹学运筹学的主要思维模式是“分析问题→建立模型→求解”，而最重要、也最难的一步是问题建模。问题建模是将语言文字上的问题转化为数学问题。虽然，实际生活中的每个问题都有其独特之处，但其中大部分还是有共性的。以下
管理运筹学从以上两例可以看出，它们都是属于同一类优化问题，其共同特征是：①每一个问题都用一组决策变量x1，x2，…，xn表示某一方案;这组决策变量的值就代表一个具体方案，一般这些变量取值是非负的。②存在一定的约束
管理运筹学对于只有两个决策变量的线性规划模型可用图解法求解。虽然图解法难以推广到多变量的情形，但能帮助我们直观地理解求解的思路，并在此启发下帮助找出更一般的求解方法。图解法具体步骤为：第一步，建立直角坐标系：以适
上一篇