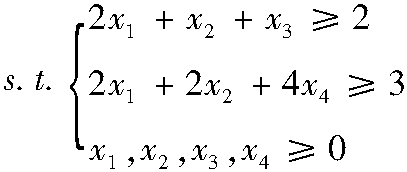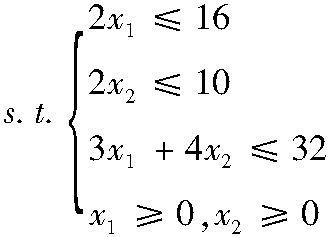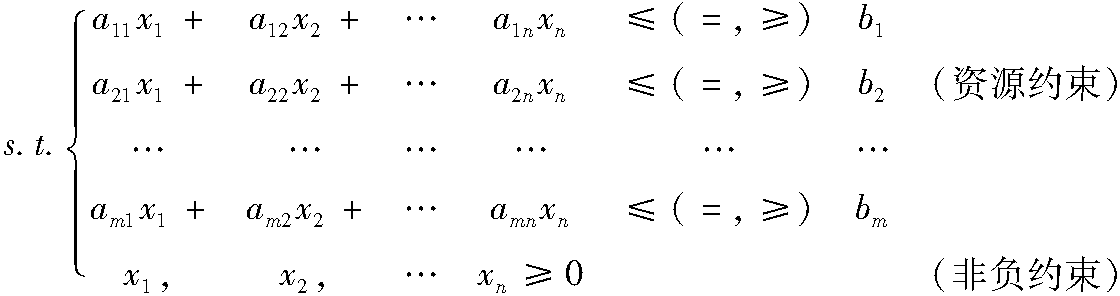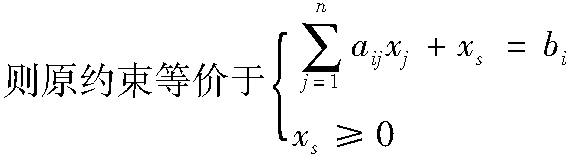
对于不符合标准型要求的一般线性规划问题，需要按以下规则进行转换为标准型：
(1)若是求minZ=cjxj，则可令z′=-z， 改求新问题的目标函数为maxZ′=(-cj)xj，则新问题与原问题同解， 只是目标函数反号而已。
(2)对于形如aijxj≤bi的约束，可引进松弛变量xs＝bi-aijxj，
(3)对于形如aijxj≥bi的约束，可引进剩余变量xr＝aijxj-bi，
(4) 若约束条件中有形如xj≥bj(bj≠0)的约束，则可令yj＝xj-bj并代入原模型中消去xj(即作平移)，这样xj≥bj便化作yj≥0。
(5) 若某决策变量xj是自由变量 (即符号不受限制)，则可引进两个非负变量x′j≥0与x″j≥0; 令xj＝x′j-x″j，代入原模型中消去xj，化为x′j≥0与x″j≥0。
(6) 当对模型中某决 ...... （共653字） [阅读本文]>>
管理运筹学运筹学的分析步骤一般包括：发现和定义待研究的问题，构造数学模型;寻找经过模型优化的结果，并通过应用这些结果来改善系统的运行效率。具体步骤如图1-1所示。1.系统分析和问题描述应用运筹学的主要目的是解决实
管理运筹学运筹学是一门以训练逻辑思维为主的课程，注重模型和定量分析方法，但又不是运筹数学;具有很强的实践性，注重原理、方法和应用，教学中对理论推导可不做过高要求。学生创造性思维培养离不开逻辑思维，但学习过程中也不
管理运筹学运筹学的主要思维模式是“分析问题→建立模型→求解”，而最重要、也最难的一步是问题建模。问题建模是将语言文字上的问题转化为数学问题。虽然，实际生活中的每个问题都有其独特之处，但其中大部分还是有共性的。以下
管理运筹学从以上两例可以看出，它们都是属于同一类优化问题，其共同特征是：①每一个问题都用一组决策变量x1，x2，…，xn表示某一方案;这组决策变量的值就代表一个具体方案，一般这些变量取值是非负的。②存在一定的约束
管理运筹学对于只有两个决策变量的线性规划模型可用图解法求解。虽然图解法难以推广到多变量的情形，但能帮助我们直观地理解求解的思路，并在此启发下帮助找出更一般的求解方法。图解法具体步骤为：第一步，建立直角坐标系：以适
上一篇