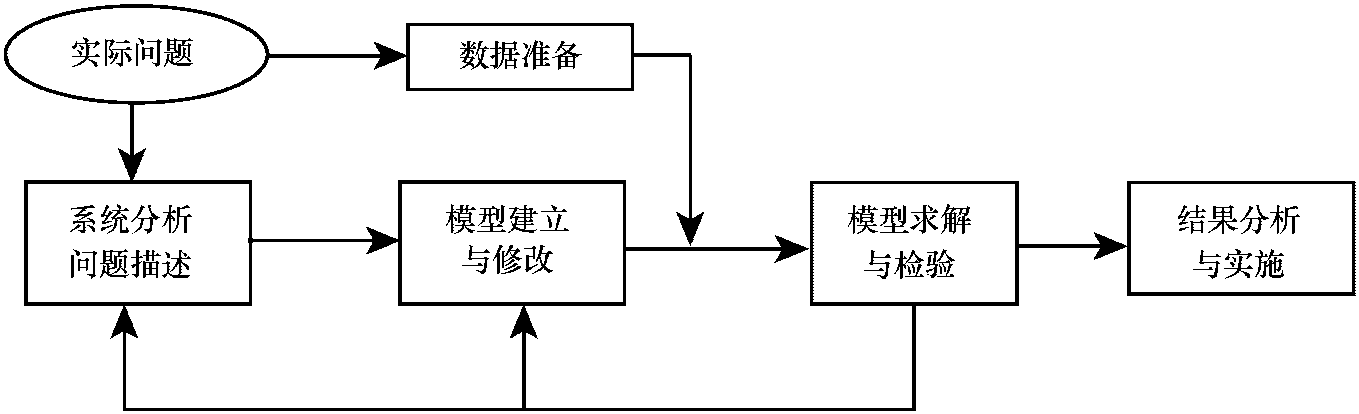
通过第二章的学习，我们已了解到通过几何做图的方法可以求得线性规划问题的最优解，而且这种方法简单直观，初学者容易接受。但是，图解法最大的不足是受维数的限制，其问题模型中变量的个数一般不能超过2个，这显然不符合实际情况，因为实际当中的问题，通常变量的个数都远远多于2个，所以我们需要另外开辟思路，寻找更通用的算法。1947年，美国学者丹捷格 (G.B. Dantzig) 提出了求解线性规划问题的单纯形方法，从理论上讲能适用任意多个变量的线性规划问题的求解。后来，库普曼 (T. C. Koopmans)和查恩斯 (A. Charnes) 对线性规划的理论和应用也做出了突出贡献。这种算法是建立在新的思路和 ...... （共337字） [阅读本文]>>
管理运筹学运筹学的分析步骤一般包括：发现和定义待研究的问题，构造数学模型;寻找经过模型优化的结果，并通过应用这些结果来改善系统的运行效率。具体步骤如图1-1所示。1.系统分析和问题描述应用运筹学的主要目的是解决实
管理运筹学运筹学是一门以训练逻辑思维为主的课程，注重模型和定量分析方法，但又不是运筹数学;具有很强的实践性，注重原理、方法和应用，教学中对理论推导可不做过高要求。学生创造性思维培养离不开逻辑思维，但学习过程中也不
管理运筹学运筹学的主要思维模式是“分析问题→建立模型→求解”，而最重要、也最难的一步是问题建模。问题建模是将语言文字上的问题转化为数学问题。虽然，实际生活中的每个问题都有其独特之处，但其中大部分还是有共性的。以下
管理运筹学从以上两例可以看出，它们都是属于同一类优化问题，其共同特征是：①每一个问题都用一组决策变量x1，x2，…，xn表示某一方案;这组决策变量的值就代表一个具体方案，一般这些变量取值是非负的。②存在一定的约束
管理运筹学对于只有两个决策变量的线性规划模型可用图解法求解。虽然图解法难以推广到多变量的情形，但能帮助我们直观地理解求解的思路，并在此启发下帮助找出更一般的求解方法。图解法具体步骤为：第一步，建立直角坐标系：以适
上一篇