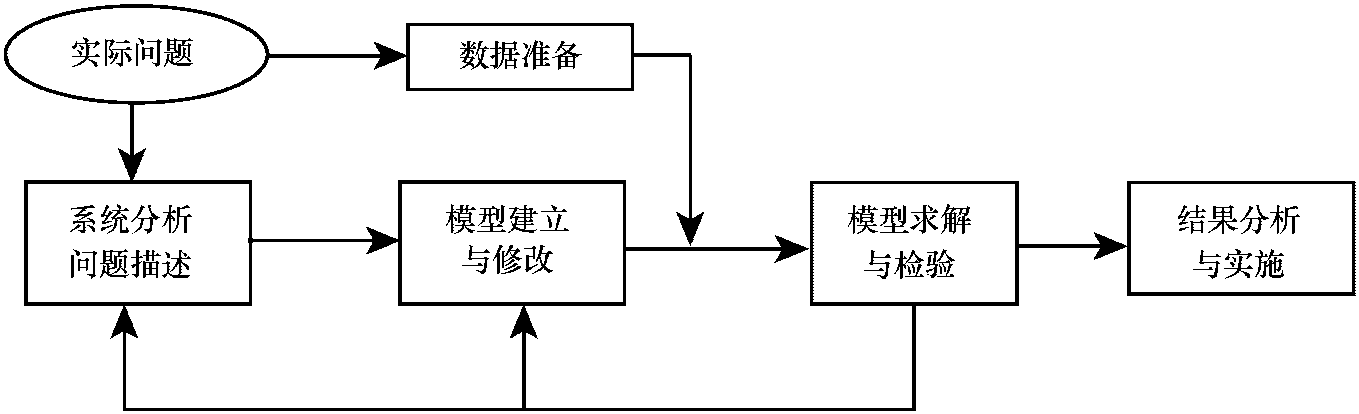
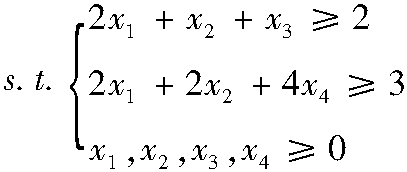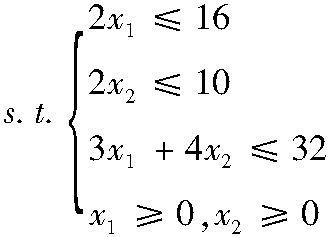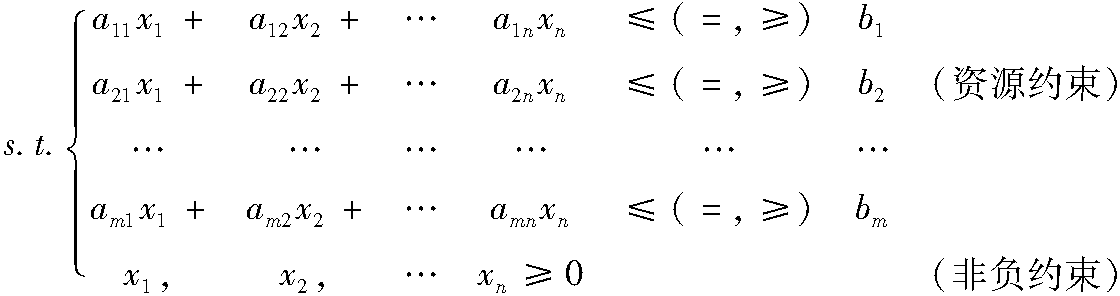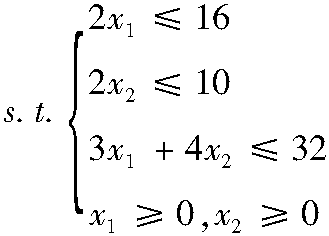2.2.3 图解法的几何意义
图解法的优点是简单直观,但由于受到维数限制,能求解问题的变量个数不能超过两个。所以说,图解法的使用是有局限性的。那么图解法的价值在哪里呢? 由图解法的求解结果可发现线性规划问题:
(1) 可行域为一个凸集。
(2) 如果有最优解,其必在可行域的某一个顶点上找到。
(3) 可行域的顶点个数是有限的。
(4) 若在两个顶点同时得到最优解,则其连线上的所有点都是最优解。
故,对一般线性规划问题要寻找最优解,只需在可行域边界的顶点上去找。将寻优问题大大简化,这才是我们学习图解法的真正价值,它为我们寻找一般算法指明了方向。对于含有三个或三个以上变量的线性规划问题通常都使 ...... (共457字) [阅读本文]>>

 上一篇
上一篇