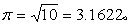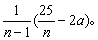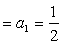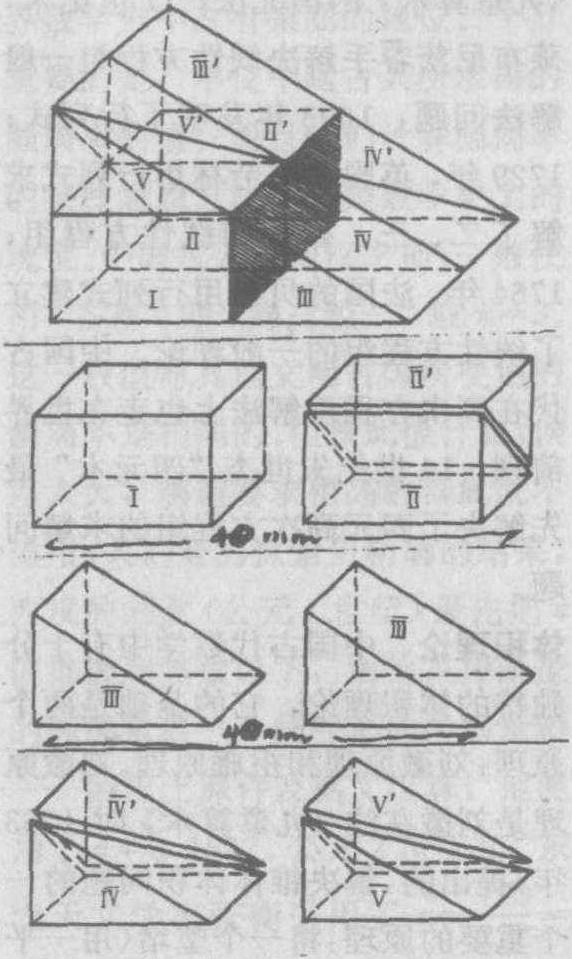
中国古代数学中有十分独特的体积理论，它的基础是两个原理：刘徽原理和祖暅原理。刘徽原理是刘徽在注《九章算术》时(263年)提出的，解决锥体体积问题的一个重要的原理：将一个壍堵(用一平面沿长方体相对两棱切割得到的楔形立体)分解为一个阳马(直角四棱锥)与一个鳖臑(四面均为直角三角形的四边体)，则阳马与鳖臑的体积比为2：1。在正方体的情况下这一原理显然成立，但长方体的情况如何呢?刘徽认为不能把正方体的情况简单地推广到长、宽、高不等的一般情况，对后者必须证明，他用极限方法证明了这一原理。他的证明用现代语言可表述如下： 用三个互相垂直的平面平分壍堵的长、宽、 ...... （共1345字） [阅读本文]>>
近现代史及国情教育圆周率是人类最早遇到的数学常量之一，自古以来世界各个地区、各个民族都对它进行过研究，并取得不同程度的成果。圆周率是圆的周长和圆的直径的比值，最先产生于制做圆形工具的需要，并且是通过测量计算出来的。测量的
近现代史及国情教育这方面中国古代取得过十分辉煌的成就。在中国古代，把开各次方和解二次以上的方程，都叫做“开方”，开方，是中国古代数学家特别擅长的课题之一。《九章算术》(公元1世纪)在世界上第一次提出完善的多位数开平方和开
近现代史及国情教育这是具有中国特色的高阶等差级数的求和问题的基本算法。在中国古代，很早就研究了一般的等差级数和等比级数，并取得一些初步的成果。如在《九章算术》中已经提出求等差级数各项以及已知首项、末项和项数求公差的问题，
近现代史及国情教育中国古人具有极其深刻的极限思想，并把这一思想用于数学中，取得一系列重要的数学成果。《庄子》中就含有相当深刻的极限思想。其中“天下篇”有这样的话：“一尺之棰，日取其半，万世不竭”。意思是，有一个一尺长的木
近现代史及国情教育十进分数的概念最早产生于中国。在古代，一般是用分数来记整数以下的奇零部分，这一点上，中外是一致的。最先提出十进分数的是中国三国时的刘徽，他在注《九章算术》(263年)时，在少广章开方术的注中提出开方不尽
上一篇