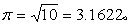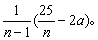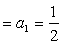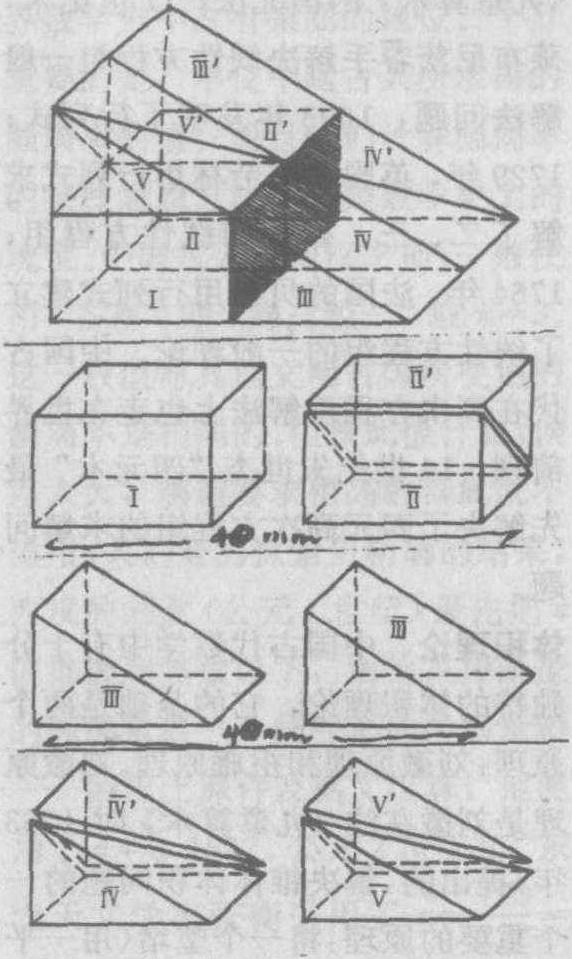
勾股定理可以说是数学中关于图形的一个基本事实，世界各文明古国对它均有研究。中国古人的勾股定理研究具有自己的特色，因而占有重要的地位。勾股定理在中国古代数学中具有十分独特的意义：理论上，它是解决许多数学问题(如“割圆术”)的重要的基本定理;应用中，它又是一种基本的数学模型，在其基础上中国古人创建的勾股测量术，使他们在测量的数学方法上长期领先于世。早在公元前11世纪，中国古人就已知了勾股定理的一个特例：52＝32+42;公元前7—6世纪，中国古人已知一般形式的勾股定理了;《九章算术》(公元1世纪成书) 中还给出了计算勾股数的一组公式。用现代数学语言表示，则 ...... （共1042字） [阅读本文]>>
近现代史及国情教育圆周率是人类最早遇到的数学常量之一，自古以来世界各个地区、各个民族都对它进行过研究，并取得不同程度的成果。圆周率是圆的周长和圆的直径的比值，最先产生于制做圆形工具的需要，并且是通过测量计算出来的。测量的
近现代史及国情教育中国古代数学中有十分独特的体积理论，它的基础是两个原理：刘徽原理和祖暅原理。刘徽原理是刘徽在注《九章算术》时(263年)提出的，解决锥体体积问题的一个重要的原理：将一个壍堵(用一平面沿长方体相对两棱切割
近现代史及国情教育这方面中国古代取得过十分辉煌的成就。在中国古代，把开各次方和解二次以上的方程，都叫做“开方”，开方，是中国古代数学家特别擅长的课题之一。《九章算术》(公元1世纪)在世界上第一次提出完善的多位数开平方和开
近现代史及国情教育这是具有中国特色的高阶等差级数的求和问题的基本算法。在中国古代，很早就研究了一般的等差级数和等比级数，并取得一些初步的成果。如在《九章算术》中已经提出求等差级数各项以及已知首项、末项和项数求公差的问题，
近现代史及国情教育中国古人具有极其深刻的极限思想，并把这一思想用于数学中，取得一系列重要的数学成果。《庄子》中就含有相当深刻的极限思想。其中“天下篇”有这样的话：“一尺之棰，日取其半，万世不竭”。意思是，有一个一尺长的木
上一篇