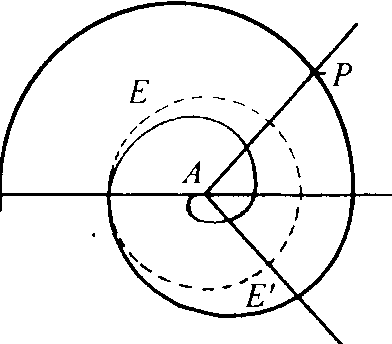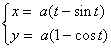
一个动圆沿同一平面内的一直线或另一圆周作无滑动地滚动时，动圆上任何点的轨迹。这种曲线首先由伽利略*提出。
动圆在直线上滚动时，形成平摆线，亦称普通摆线，即通常所说的摆线。
平摆线的参数方程为
1501年布埃莱斯(C.Bouvillus 1470—1553)从圆化方问题*引入这种曲线，但系统的研究开始于1628年。此后人们发现了它的许多有趣性质。例如，摆线是最速降线*等。普通单摆的周期与摆动的幅度有关。为了克服这个缺点，如果在摆动平面内做两个摆线形状的挡板，摆的运动轨迹将仍是一条摆线，摆线的名称由此而来。沿摆线弧摆动的摆锤，无论摆动幅度多大，摆动周期完全相同，因此亦称为等时曲线 ...... （共361字） [阅读本文]>>
简明数学汉英群论*证明了五次或五次以上的一般代数方程的解无法用根式表出，即不能通过对方程系数进行有限次代数运算得到。他还完成了一般情况下(包括复指数)二项式(乘幂)展开定理的证明。阿贝尔
简明数学汉英生于叙拉古(意大利西西里岛东南部，当时希腊的殖民城市)。古希腊著名学者;人类历史上最伟大的数学家、物理学家之一;力学的奠基人。他曾研究出如何确定圆、圆锥曲线和螺线*。他是世界上最早运用微积分思想的科学
简明数学汉英在同一平面，一动点P沿动射线AP作匀速直线运动;同时，射线AP又绕A点旋转，则P的轨迹为螺线。当AP以等角速度绕A点旋转时，P的轨迹就是阿基米德螺旋线。阿基米德螺旋线
简明数学汉英古希腊著名数学家及天文学家。他生活并工作在萨摩斯岛。在哥白尼建立日心说之前八百年，他首先提出了地球绕太阳运行的观点。他已经知道地球是圆球形的;算出了一年的时间有多长。他曾测算出太阳到地球与月球到地球距
简明数学汉英芝诺悖论之一。艾基利斯是荷马史诗《伊利亚特》中的希腊英雄，以善跑着称。芝诺据此提出的悖论是，在赛跑中，只要让乌龟先跑一段路程，那么，无论艾基利斯跑得多快，也追不上这只乌龟。因为当艾基利斯赶上这段路程时
上一篇