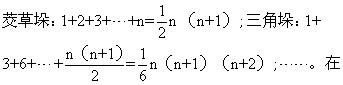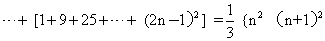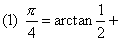一卷。清梅文鼎 (详见 《历算全书》)撰。欧几里得 《几何原本》经徐光启、利玛窦译出前六卷之后，立即引起了梅文鼎的兴趣，梅文鼎认为我国传统的勾股算术和由西洋传入的《几何原本》形式上虽不相同，但理论可以会通。在梅氏 《勿庵历算书记》中他指出：“几何不言勾股，然其理并勾股也。〔此言勾股西谓直角三边形，译书时未能会通，遂分途径〕。故其最难通者以勾股释之则明。”《几何通解》就是为达“以勾股释之”而作，他依据勾股算术证明了 《几何原本》卷二至卷六中的许多命题。例如卷三第三十五题论证： 圆内二弦AB、CD交于E，则AE·EB=CE·ED。梅文鼎以勾股术证明如下(译成今文) ...... （共1005字） [阅读本文]>>
四库一卷。明徐孝编、张元善校。徐孝，明末顺天(今北京市)人，不仕。著《合并字学集篇集韵》二十三卷，《重订司马温公等韵图经》即是书所附之韵表。张元善永城(今河南永城县)人，彭城伯骐之后，袭封惠安伯。张氏卒于万
四库八卷。元丁巨(生卒年不详)撰。丁巨始末未详，在《丁巨算法》自序中，丁巨记载了成书经过：“独余幼贱，不伍时流，经籍之余事。法物度轨，则间尝用心。因于算术上自九章，下至小法，数十百家，摘取要略。述算法八卷。
四库一卷。清陈世仁(1676—1722)撰。陈世仁字元之，号焕吾，浙江海宁人，系陈訏的族侄，好学工为文，精晓算学。康熙五十四年(1715)以进士入翰林后，即回乡不仕。《少广补遗》专论垛积之术，视垛积为少广，
四库三卷。清邹伯奇(1819—1869)撰。邹伯奇，字特夫，又字一鹗，广东南海人，通经博古，尤擅算学，与夏鸾翔、丁取忠等名家交往甚密，在南方沿海诸省颇负盛名。曾于1866和1868年两度被朝廷召任北京同文馆
四库一卷。清曾纪鸿(1848—1877)撰。曾纪鸿，字栗诚，湖南湘乡人，曾国藩次子，丁取忠的学生，曾与黄宗宪、左潜于丁取忠指导下在长沙古荷花池的白芙堂共同研究数学。与丁取忠等同撰《粟布演草》第一卷、《对数详
上一篇