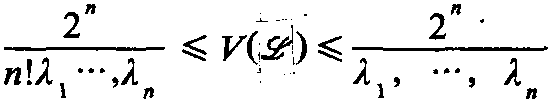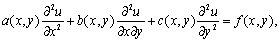包括一个自变量和它的末知函数以及未知函数的微商的等式，是微分方程的分支。常微分方程的基本问题在于求解和研究解的各种属性。在数学中，它是研究几何对象 (曲线、曲面及更一般的空间形式) 以及某些代数对象 (连续群等) 的基本工具之一。也是研究力学、电子技术、自动控制、星际航行等各个学科的必需的工具。
常微分方程的发展经历了实域解析理论、复域解析理论及实域定性理论三个阶段，并发展为三个主要方向： 解析方法、几何方法 (又称定性方法) 及数值方法。由于人类探索自然现象和社会现象的确定性运动规律的需要，常微分方程不断面临新的研究课题。复域定性研究是一个刚刚 ...... （共465字） [阅读本文]>>
自然科学学科用几何方法研究某些数论问题的数学理论。又称几何数论，数论的分支学科。是研究丢番图逼近、代数数论的重要工具。它的一类典型问题为：设f(x1，…，xn)是实变量x1，…，xn的实值函数，则对适当选取的整数u
自然科学学科含有未知函数的偏导数的方程称为偏微分方程，是微分方程的分支。含于方程中的偏导数的最高阶称方程的阶。例如，即为关于未知函数u(x，y)的二阶偏微分方程。二阶线性与非线性偏微分方程始终是重要的研究对象。这类
研究现实世界中数量关系和空间形式的科学。简言之，数学是研究数和形的科学。它的特点是：抽象性、精确性和应用的广泛性。数学的抽象性表现在它暂时撇开事物的具体内容而单纯从量的关系来考察;精确性表现在它的逻辑的
研究数的规律，特别是研究整数规律的科学。数学的分支学科。数论以可除性、同余性、不定方程的求解和数的有理逼近等算术问题为研究对象，是两个最古老的数学分支之一(另一个是经典的欧氏几何)。正整数分成1、素数和
用分析方法研究整数的性质和素数分布规律的科学。数论的分支学科。解析数论以素数分布、格点问题和堆垒数论中的问题为主要的研究对象。一般说来，凡是用分析方法研究的数论问题都可归结为解析数论，解析数论的内容十分
上一篇