第四节 常用的数学公式
分类：线损管理1124字
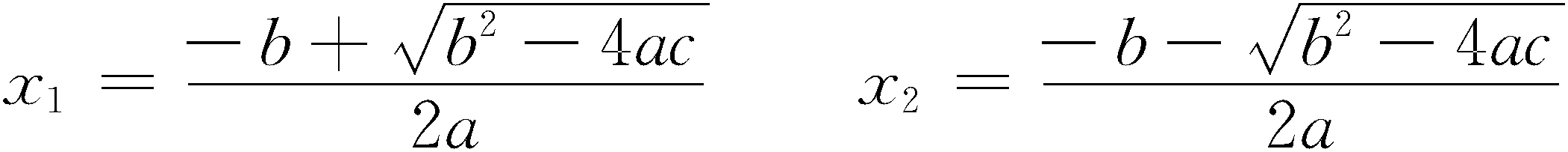
1.展开式
(x+a)(x+b)=x2+(a+b)x+ab
(a±b)2＝a2±2ab+b2
(a±b)3＝a3±3a2b+3ab2±b3
(a+b+c)2＝a2+b2+c2+2ab+2bc+2ca
(a+b+c)3＝a3+b3+c3+3a2b+3ab2
+3b2c+3bc2+3a2c+3ac2+6abc
a2-b2＝(a-b)(a+b)
a3±b3＝(a±b)(a2 ∓ ab + b2)
a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca)
a4+a2b2+b4＝(a2+ab+b2)(a2-ab+b2)
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
2.二次方程式
ax2+bx+c=0，a、b、c是实数，且a≠0
则该方程的根为
且根与系数的关系为 判别式为b2-4ac
3.指数定则
m、n为正整数，a、b为正实数，则
am×an＝am+n
＝am-n
(am)n＝amn
(a×b)n＝an×bn
a-n＝
a＝＝()m
×＝
＝
＝
a0＝1
4.对数定则
设x、y、a、b、c为正实数，则
5.级数定则(1)等差级数
(2)等比级数 (3)数列前n项的和6.二项式定理(a+b)n＝ an + nan-1b +an-2b2
+an-3b3+…
+ an-kbk+…+bn
7.复数
i=; ...... （共1124字） [阅读本文]>>
上一篇
.jpg)
.jpg)
